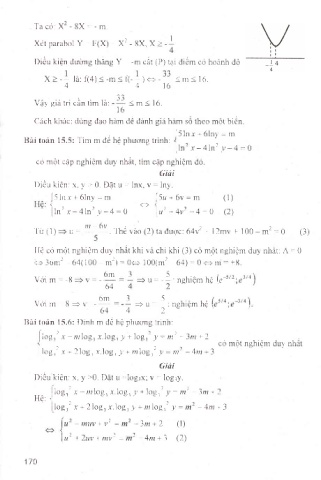Page 171 - Phương Trình Mũ Logarit

Ta có: X - 8X = - m.
1
Xét parabol Y = F(X) = x^ - 8X, X > -

Điều kiện đường thẳng Y = -m cắt (P) tại điểm có hoành độ

x > - - l à : f ( 4 ) < - m < f ( - - ) < í : > - — < m < 16.
4 4 16
. . X 33
Vậy giá trị cân tìm là: < m < 16.
16
Cách khác: dùng đạo hàm để đánh giá hàm sổ theo một biến.
Í51nx + 61ny = m
Bài toán 15.5: Tìm m để hệ phương trình:
[ l n - x - 4 1 n \ v - 4 = 0
có một cặp nghiệm duy nhất, tìm cặp nghiệm đó.
Giải
Điều kiện: X , y > 0. Đặt u = Inx, V = Iny.
Í51nx + 61ny = m Í5M + 6v = m (1)

ị l n ' x - 4 1 n ' y - 4 = 0 ^ | m ' - 4 v - - 4 = 0 ( 2 )
m - 6 v
T ừ ( l ) u = . Thế vào (2) ta được: 64v^ + 12mv + 100 - m^ = 0 (3)

Hệ có một nghiệm duy nhất khi và chỉ khi (3) có một nghiệm duy nhất: A = 0
m^) = 0 « 100(m^-
o 36m^ — 64(100 — m^) = 0<=> 100(m^ — 64) = 0 o rri -- ±8.
6m 3 5
Với m = -8 V = - - u = -—: nghiệm hệ [ e
64
6m 3 5
V ớ i m = 8 ^ v = - — => u = - : nghiệm hệ
64 4 2 ^ ^ ’ ’
Bài toán 15.6: Định m để hệ phương trình;
Ịlog3^ x - f f í l o g 3 x.log3 _y + log3“ y = m^ - 3m + 2
có một nghiệm duy nhất
^log,^ x + 21og3 x.log, y + m\og^^ y = nr - Am+ 2
Giải
Điều kiện: X , y >0. Đặt u =log3x; V = log3y.
2 2 2
log3 X - w l o g 3 x.log3 y + log3 y = m -3m + 2
Hệ:
log3^ x + 21og3 x.logj y + m\og^^ y = -4 m + 3

I - muv + v^ = -3m + 2 (1)

[ u ^ + 2 u v + m v ^ = - A m + 3 (2)

170