Page 90 - Bộ Đề Toán Luyện Thi THPT

LỜI GIẢI
Câu 1.
. Tập xác định: D = R. Hàm số chẵn.
• Sự biến thiên: lim y = lim y = +C0
X->-co X->+00
y’ = 8x^ - 8x; y' = 0 <=> X = 0 hoặc X = ±1
—00 - 1 0 1 +CC
X
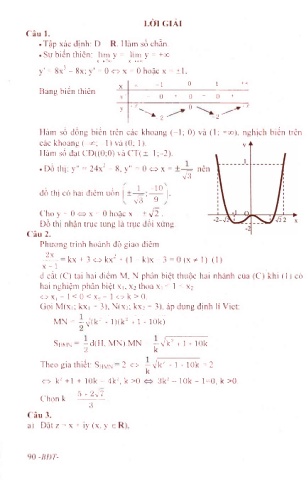
Bảng biến thiên
y ’ - 0 + 0 - 0 +
+ 00 ^^+00
y r °
^ - 2 ' - 2 "
Hàm sổ đồng biến trên các khoảng (-1; 0) và (1; +oo), nghịch biển trên
các khoảng (-ũo; - 1 ) và (0; 1).
Hàm số đạt CĐ((0;0) và CT( + 1 ;-2).

. Đồ thi: y" = 24x^ - 8, y" = 0 ^ X = nên
Vs
1 -10
đồ thị có hai điểm uốn
V s’ 9

Cho y = 0 Cí> X = 0 hoặc X = ± ^Ỉ2 .
Đồ thị nhận trục tung là trục đối xứng.
Câu 2.
Phương trình hoành độ giao điểm
2x
kx + 3c:>kx^ + ( l - k ) x - 3 = 0 ( x ^ l ) ( 1 )
x - 1
d cất (C) tại hai điểm M, N phân biệt thuộc hai nhánh của (C) khi (1) có
hai nghiệm phân biệt X|, Xi thỏa X| < 1 < X2
o x i - l < 0 < X 2- l < = > k > 0.
Gọi M(xi; kxi + 3), N(X2; kx2 + 3), áp dụng định lí Viet:

M N= -7 (k ^ + l)(k‘'' + l + 10k)

Smmn -d iH , MN).MN = -V k ^ T ĨT ĩÕ k
2 k
Theo giả thiết: SiiMN 2 « -V k^ + l + 10k = 2
k
o k''" +1 + lOk = 4k^ k >0 3k'' - lOk - 1=0, k >0.
^ = 5 + 2^/7
Chọn k = ---------- .
3
Câu 3.
a) Đặt z = X + iy (x, y e R),

90 -BĐT-