Page 333 - Bộ Đề Toán Luyện Thi THPT

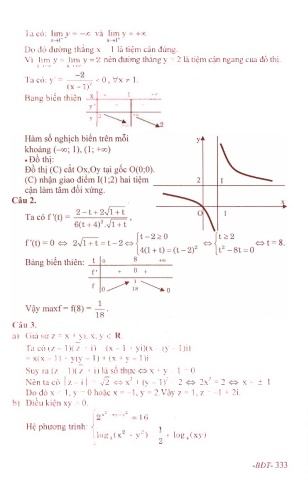
Ta có: lim v = - 0 0 và lim y = +oo

Do đó đường thẳng X = 1 là tiệm cận đúng.
Vì lim y = lim y - 2 nên đường thẳng y = 2 là tiệm cận ngang của đồ thị.
X -> -c o X ^ -H »
Ta có: y' = -----r- < 0, Vx 5^ 1.
(x-1)^ -00 1 +Q0
Bảng biến thiên X
y’ - -
y 2 +00
— 00

Câu 3.
a) Giả sử z = X + yi, X, y e R.
Ta có (z - 1)(z + i) = (x - 1 + yi)(x - (y - 1 )i)
= x(x - 1) + y(y - 1) + (x + y - 1 )i
Suy ra (z - 1)(z + i) là số thực X + y - 1 = 0
Nên ta có 1 z - i I = %/2 <=> x^ + (y - 1 )^ = 2 2x^ = 2 X = ± 1
Do đó X = 1, y = 0 hoặc X = -1, y = 2.Vậy z = 1, z = -1 + 2i.
b) Điều kiện xy > 0.
9
2
(X^^-xy + y'^ _
16
Hệ phưong trình:
2 '
log^Cx + y ) = " + log4 (xy)
ù
-BĐT- 333