Page 327 - Bộ Đề Toán Luyện Thi THPT

x-V y+2=-
Câu 9. (1 điểm) Giải hệ phương trình: < (x, y e R).
y+ 2(x - 2)Vx + 2 = - -

Câu 10. (1 điểm) Cho X, y, z là các số thực không âm phân biệt. Chứng minh
Ị x + y y + z z + X 9
răng: ------ ~Õ ---------õ" --------- õ" ^ ----------- ■
( x - y ) ( y - z ) ^ ( z - x ) ^ x + y + z

LÒI GIẢI
Câu 1.
Hàm số: y = - 2x^ + 1.
• Tập xác định; D = R
. Sự biến thiên:
/ 2
lim x^ 1 - 1 ìl = ±00
V
X ->±00 X X'" )\
y ' = 3x^ - 4x, y ' = 0 <=> X = 0 hay X = - .
3
Bảng biến thiên:
X +0O
y' 0 - 0

5
' 2 7
' ,44 4
Hàm sô f tăng trên các khoảng (-0 0 ; 0), (—;±Q0 ); giảm trên (0; —). Hàm
3 3
' ’ 4 4 ■ 5
sô đạt cực đai tại X = 0, y(0) = 1, đạt cực tiêu tai X = —, y(—) = —— .
4 3 3 2T
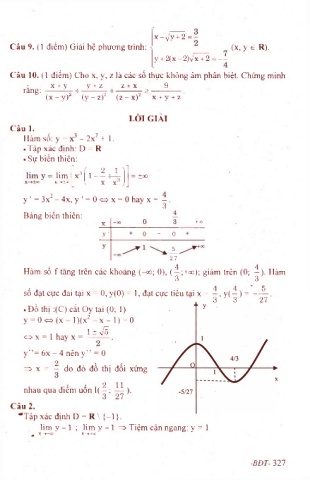
• . Đồ thị ;(C) cắt Oy tại (0; 1) L/o ini ) cai uy lại 1 )
y = 0<=>(x - l)(x ^ -x - í) = 0
1 ± S
<=> X = 1 hay X =
y” = 6 x - 4 n ê n y ” = 0
2
=> X = — do đó đô thị đôi xứng

2 11
nhau qua diêm uon I( ^ ; - ^ ).
3 27
Câu 2.
*Tập xác định D = R \ (-1}.
lim y = 1 ; lim y = 1 => Tiệm cận ngang: y = 1
^ X -+ -0 0 X ->+00

-BĐT- 327