Page 318 - Bộ Đề Toán Luyện Thi THPT

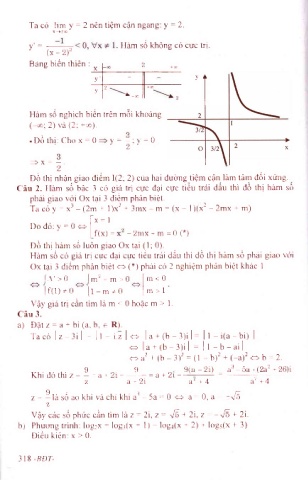
Ta có lim y = 2 nên tiệm cận ngang; y = 2.
X->±co
Hàm số không có cực trị.
y ' = — — —
^ (x-2)^
Bảng biến thiên : X ỉ +00
y' - y Ạ
y 2 ^ —co +00
2

Hàm số nghịch biến trên mỗi khoảng
(-00; 2) và (2; +co).

. Đồ thị: Cho X = 0 y = f ; y = o

^ X = - .
2
Đồ thị nhận giao điểm 1(2; 2) của hai đường tiệm cận làm târn đối xứng.
Câu 2. Hàm sô bậc 3 có giá trị cực đại cực tiêu trái dâu thì đô thị hàm sô
phải giao với Ox tại 3 điểm phân biệt.
Ta có y = x^ - (2m + ])x^ + 3mx - m = (x - ])(x^ - 2mx + m)
x - 1
Do đó: y = 0 <»
f(x) = - 2mx + m = 0 (*)
Đồ thị hàm sổ luôn giao Ox tại (1; 0).
Hàm số có giá trị cực đại cực tiểu trái dấu thì đồ thị hàm số phải giao với
Ox tại 3 điểm phân biệt <=> (*) phải có 2 nghiệm phân biệt khác 1
ÍA’>0 í m ^ - m > 0 r m < 0
[f(l)7t0 Ịl- m ;tO L m > l

Vậy giá trị cần tìm là m < 0 hoặc m > 1.
Câu 3.
a) Đặt z = a + bi (a, b, e R).
Ta có 1 z - 3i I = 1 1 - i.z I <» 1 a + (b - 3)i I = I 1 - i(a - bi) I
Cí> I a + (b - 3)i I = I 1 - b - ai 1
« a^ + (b - 3)^ = (1 - b)^ + (-a)^ « b = 2.
9 . . 9 9 (a -2 i) _ a^-5a+(2a^+26)i
Khi đó thì z - — = a + 2i - ■ • = a + 2 i------------- -------------- ÍT—:--------
z a + 2i a" +4 a^ +4
9 ' 3 Ị—
z - — là sô ảo khi và chỉ khi a -5 a = 0 < = > a = 0 , a = ± v 5
z
Vậy các số phức cần tìm là z = 2i, z = yíE + 2i, z = -yỊE + 2i.
b) Phương trình: log2X + log3(x + 1) = log4(x + 2) + log5(x + 3)
Điều kiện: X > 0.

318 -BĐT-