Page 247 - Bộ Đề Toán Luyện Thi THPT

• Tập xác định: D = R: Hàm số chẵn.
• Sự biến thiên: lim y = - 0 0 .
X -> ± 0 0
y' = -x^ + 3x = x(3 - x^) = 0 <=> ± Vs hoặc X = 0.
y' > 0 <:í> X = -yỈ3 hoặc 0 < X < Vs .

Bảng biến thiên: x — 00 -Vã 0 +00

y' + 0 - 0 + 0 _
y 9
— 00 ✓ 4 ^ 0 / 4 ^ -00
^
Hàm số đồng biến trong các khoảng (-oo; - V ã) và (0; Vs ) ; nghịch biến
ữong các khoảng (- Vs ; 0) và ( Vs ; +ũo).
' ’ r 9
Hàm sô đạt cực đại tại điêm (± V3; —) và cực
tiểu tại điểm (0 ;0).
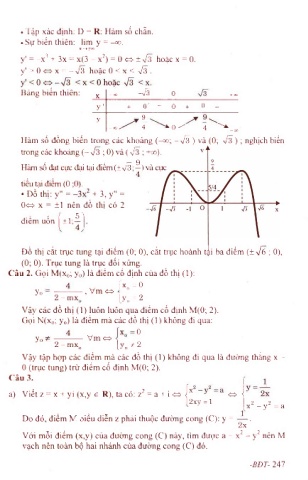
• Đồ thị: y" = + 3, y" =
O o X = ±1 nên đồ thị có 2
' 5^
điểm uốn ± 1; -

Đồ thị cắt trục tung tại điểm (0; 0), cắt trục hoành tầi ba điểm (±V6 ; 0),
(0; 0). Trục tung là trục đối xứng.
Câu 2. Gọi M (X o ; yo) là điểm cố định của đồ thị (1);
[ X o - 0
yo^ , V m <tí>
2 - m x , l y o = 2
Vậy các đồ thị (1) luôn luôn qua điểm cố định M(0; 2).
Gọi N(Xo; yo) là điểm mà các đồ thị (1) không đi qua:
yo — Vm <z> ^
2 - m x „ ^ ly o ^ 2
Vậy tập hợp các điểm mà các đồ thị (1) không đi qua là đường thẳng X =
0 (trục tung) trừ điểm cố định M(0; 2).
Câu 3.

a) Viết z = X + yi (x,y e R), t a c ó : z ^ = a + i< :í'J^ <=> i
12xy = 1
x ^ -y ^ = a
Do đó, điểm V oiểu diễn z phải thuộc đường cong (C): y = .
2x
Với mỗi điểm (x,y) của đường cong (C) này, tìm được a = x^ - y^ nên M
vạch nên toàn bộ hai nhánh của đường cong (C) đó.

-BĐT- 247