Page 231 - Bộ Đề Toán Luyện Thi THPT

độ các đỉnh của hình chữ nhật.
•I f Ị- \ 4
C âu 9. ( 1 đ iêm ) G iải bát phương trình; 2x + 5v X > 1 1 + .
X - 2
C âu 10. (1 điểm ) Cho các số thực không âm a, b, c thoả mãn a+b+c =1. Tìm giá trị
nhỏ nhất cìia biểu thức M = 3(a^b^ + b^c^ + c^a^) + 3(ab+ b c + ca) + 2\la^ +b^ +c^

L Ò I G IẢ I
C âu 1.
• Tập xác định: D = R . H àm số chẵn.
• Sự biến thiên: lim y = + 00.
X ->±00
y' = 4x^ - 8x = 4x(x^ - 2), y' = 0 <=> X = 0 hoặc X = ± ^/2 .
B ảng biến thiên:
X —00 0 V 2 +”
y ' - 0 + 0 - 0 +
+00 .
y

H àm số đồng biến trên các khoảng (-2 ; 0) và (2; +oo), nghịch biến trên
các khoảng (-oo; - y p ĩ) và (0; y í ĩ ).

H àm số đạt C Đ (0; 0), đạt C T (-V 2 4), ( V 2 ; -4 ).
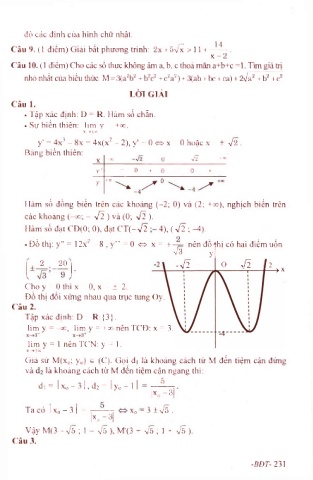
• Đ ồ thi: y" = 1 2 x ^ - 8 , y ” = 0 » X = ± ~ nên đồ 4hị có hai điểm uốn
V3
y
2 _ w -V2 o J ĩ h

C ho y = 0 thì X = 0, X = ± 2.
Đ ồ thị đối xứ ng nhau qua trục tung O y.
C âu 2.
Tập xác định: D = R \ { 3 } .
lim y = - 00, lim y = + 0 0 nên TC Đ : X = 3.
lim y = 1 nên TC N ; y = 1.
X^±oo
G iả sử M(Xo; yo) e (C ). G ọi di là khoảng cách từ M đến tiệm cận đứng
và là khoảng cách từ M đến tiệm cận ngang thì:
d i = | x o - 3 l , d 2 = l y o - 1 I ^
| x o - 3 |

Ta có I Xo - 3 I = \o ~ 3 àz\/E .
|xo -3 |

V ậy M (3 -^ /5 ; 1 - n/5 ), M '(3 + Võ ; 1 + Võ ).
C âu 3.

-BĐT-23\