Page 221 - Bộ Đề Toán Luyện Thi THPT

đường tròn tâm I tiếp xúc với cả hai đường tròn (S|), (S2), biết tâm I
thuộc đường thẳng d: X - y = 0.
X + 2 x - 8
Câu 9. (1 điểm) Giải phưong trình: = (x + l)(Vx + 2 - 2), X 6 R.
■ 2x + 3
X" -z x + a
Câu 10. (1 điểm) Cho các số thực dương a, b, c.Tìm giá trị nhỏ nhất của
. a, 1
„2 . 2 / 3
________ ________ 4 c-
biểu thức: p
(a + b )' ^ (b + c)''' ^ 3(c + a)"

LỜI GIẢI
Câu 1 .. Tập xác định: D = R
. Chiều biến thiên:
lim y = +00 , lim y = -co

y' = -3x^ + 6x; y' = 0 <=í> X = 0 hoặc X = 2
y(0) = 0,y(2) = 4
X —00 0 2 +00
Bảng biến thiên;
y ' - 0 + 0 -
4
y
^ 0

Hàm số đồng biến trên khoảng (0; 2) và nghịch biến trên mỗi khoảng
(-co; 0), (2 ; +00)
Hàm số đạt cực tiểu tại X = 0 và ycT = 0,
đạt cực đại tại X = 2 và ycn = 4.
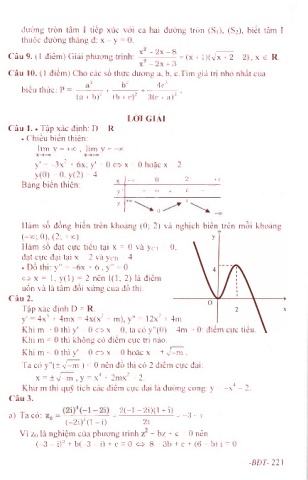
. ĐỒ thị: y" = - 6x + 6 , y" = 0
<=> X = 1, y ( l ) = 2 nên 1(1; 2) là điểm
uốn và là tâm đối xứng của đồ thị.
Câu 2.
Tập xác định D = R.
y’ - 4x^ + 4mx = 4x(x^ + m), y" = 12x^ + 4m
Khi m > 0 thì y' = 0 <=> X = 0, ta có y"(0) = 4m > 0; điểm cực tiểu.
Khi m = 0 thì không có điểm cực trị nào.
Khi m < 0 thì y' = 0 o X = 0 hoặc X = ± V-m .
Ta có y"(± V-m ) < 0 nên đồ thị có 2 điểm cực đại:
X = ± V-m , y = x‘* + 2mx^ - 2.
Khừ m thì quỹ tích các điểm cực đại là đường cong: y = -x"* - 2.
Câu 3.
a) Ta có: = M z |X l ± 2 ) = - 3 - i
(-2i ) ' ( l - i ) 2i
Vì zo là nghiệm của phương trình + bz + c = 0 nên
(-3 - i)^ + b(-3 - i ) + c = 0<:í> 8 - 3 b + c + ( 6 - b ) i = 0

-BĐT-22Ì