Page 216 - Bộ Đề Toán Luyện Thi THPT

đưÒTig cao hạ từ đỉnh c đi qua điểm M (l; 3). Diện tích tam giác ABC
bàng 2 và đường thẳng BC: X + y - 4 = 0. Tìm tọa độ của đỉnh B và c.
Câu 9. (1 điểm) Giải hệ phương trình:
x^(l + y^) + y^(l + x^) = 4ựxỹ
r—— ;------ - „ , (x, y e R).
x^y-y/l + y^ - V ĩ + x ^ = x ^ y - X
Câu 10. (1 điểm) Cho X, y, z là các số thực không âm thoả mãn:
X + y + z = 2. Chứng minh rằng x^y + y^z + z^x + xy^ + y^z + zx^ < 2.

LỜI GIẢI
x"*
Câu 1. Hàm số: y = - — 2x^ + 4 .

. Tập xác định: D = R. Hàm số chẵn.
• Sự biến thiên: lim y = +00.
X->±00
y' = x^ - 4x = x(x^ - 4), y' = 0 <=> X = 0 hoặc X = ±2.
Bảng biến thiên: _x_' —00 -2 0 2 +00
X
y' - 0 4- 0 - 0 +
+00
y 4 ^
0
^ 0
Hàm số đồng biến trên các khoảng (-2; 0) và (2; +Q0), nghịch biến trên
các khoảng (-oo; - 2) và (0; 2). ị ± _ ?__ . ’ ^ ^
l v T
Hàm số đạt CĐ(0; 4), đạt CT(-2; 0), (2; 0).
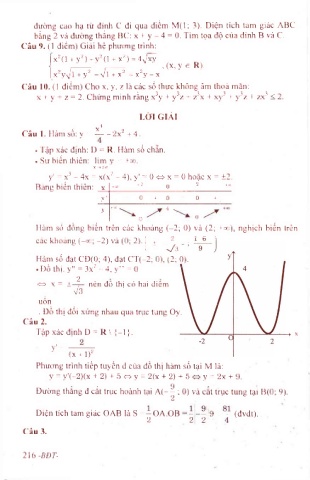
. Đ ồ t h ị : y " = 3 x ^ - 4 , y ” = 0
2
<=> X = ± nên đô thị có hai điêm
Vã
uốn
. Đồ thị đối xứng nhau qua trục tang Oy.
Câu 2.
Tập xác định D = R \ {-1}. > X
y' = — -—
(X + I)^
Phương trình tiếp tuyến d của đồ thị hàm số tại M là:
y = y'(-2)(x + 2) + 5 o y = 2(x + 2) + 5 y = 2x + 9.
' 9
Đường thăng d căt trục hoành tại A (-— ; 0) và căt trục tung tại B(0; 9).
2
Diện tích tam giác OAB là s = —OA.OB ;9|=— (đvdt).
2 2 2
Câu 3.

216 -BĐT-