Page 160 - Bộ Đề Toán Luyện Thi THPT

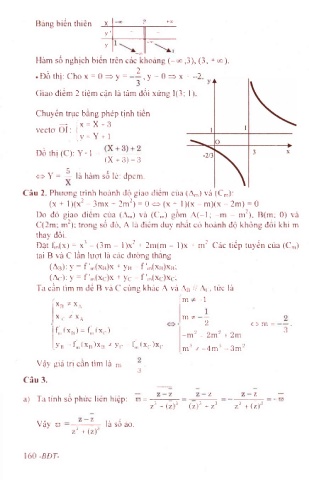
Bảng biến thiên X c I +00
.V' - -
+ 00
y
Ơ3
Hàm số nghịch biến trên các khoảng ( - 0 0 ;3), (3 , + oo).
1 r 2
• Đồ thị: Cho X = 0 ^ y = ,y = 0 = ỉ > x = - ~
Giao điểm 2 tiệm cận là tâm đối xứng 1(3; 1)

Chuyển trục bằng phép tịnh tiến
—; íx = X + 3
vectơ 0 1 : (
[y = Y + l
ĐỒ thi (C): Y+1 =
^ (X + 3 ) - 3
5
» Y = — là hàm sô lẻ: đpcm.

Câu 2. Phương trình hoành độ giao điểm của (Am) và (Cm):
(x + l)(x^ - 3mx + 2m^) = 0 C5- (x + l)(x - m)(x - 2m) = 0
Do đó giao điểm của (Am) và (Cm) gồm A (-l; -m - m^), B(m; 0) và
C(2m; m^); trong số đó, A là điểm duy nhất có hoành độ không đổi khi m
thay đổi.
Đặt fm(x) = x^ - (3m - 1 )x^ + 2m(m - l)x + m^, Các tiếp tuyến của (Cm)
tại B và c lần lượt là các đường thẳng
(Ab): y = f'm(XB)x + yB - f'm(XB)XB;
(Ac); y = f'm(xc)x + yc - f'm(xc)xc;
Ta cần tìm m để B và c cùng khác A và Ab // Ac, tức là
m - 1
Xr ^x^
X'C ^ Xa m ^ —
2 <=> m = .
3
C ( X b ) = C ( X c ) -m^ = 2m^ + 2m
Yb - C ( x b ) x b ^ Yc -C (xc)xc m^ ^ -4m^ - 3m^

Vậy giá trị cần tìm là m = - —.
3
Câu 3.

a) Ta tính số phức liên hiêp: t3 = — ^ ^ ^ -ĩij
z^+(zý ( z ) ' + z ' z ' + ( z ) '

Vậy T3 - í — l à s ố ả o .
z ^ + ( z ) ^

160 -BĐT-