Page 114 - Bộ Đề Toán Luyện Thi THPT

LỜI GIẢI

Câu 1, Hàm số: y = + 3x - 4.
• Tập xác định: D = R
• Sự biến thiên: lim y = +00 và lim y = -00
X->-00
y'= -x^ - 2x + 3; y' = 0 <=> X = 1 hoặc X = -3.
y' > 0 <=> X e (-3; 1); y' < 0 o X € ( - 00; -3) u (1; +Q0).
Bảng biến thiên:
X -00 - 3 1 +00
y' 0 + 0 -
hoo ^
y
^ - 1 3 ^

-3) và (1; +oo).
7
Hàm sô đạt cực đại tại: X = 1, y c Đ “ y(l) = - —
Hàm sổ đạt cực tiểu tại: X = 3, ycT = y(-3) = -13.
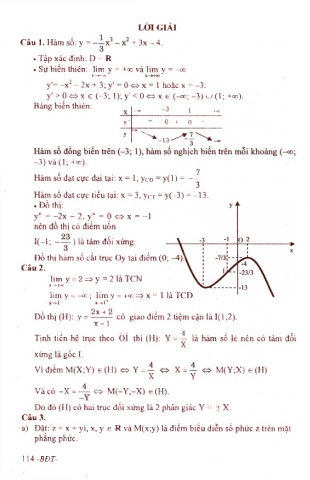
• Đồ thị:
y" = -2x - 2, y" = 0 » X = -1
nên đồ thị có điểm uốn
I( -l; ) là tâm đối xứng.

Đồ thị hàm số cắt trục Oy tại điểm (0; -4))
Câu 2.
lim y = 2 = > y = 21àTCN
X-*»±oo
lim y = - 00; lim y = +00 => X = 1 là TCĐ
« ^1“ . »1+
x^r
' 2x ^ 2 *
Đô thi (H): y = ——— có giao điêm 2 tiêm cân là 1(1 ;2).
X - 1
„ ' — • 4 í
Tịnh tiên hệ trục theo 01 thì (H): Y = — là hàm sô lẻ nên có tâm đôi
X
xứng là gốc I.
VìđiểmM (X;Y) e ( H ) o Y = - x=— M(Y;X) e ( H )
X Y

Và có -X = — ^ M (-Y;-X) e (H).
Do đó (H) có hai trục đối xứng là 2 phân giác Y = ± X.
Câu 3.
a) Đặt: z = X + yi, X, y e R và M(x;y) là điểm biểu diễn số phức z trên mặt
phăng phức.

\\4-BĐT-