Page 104 - Bộ Đề Toán Luyện Thi THPT

đường thẳng (d); X - >/2y + 2 = 0 d c ắ t (E) tại B, c. Tìm điểm A e (E)
để diện tích tam giác ABC đạt giá trị lớn nhất.
Câu 9. (1 điểm) Giải bất phương trình V õ x -l - Vx -1 > V 2 x - 4 .
Câu 10. (1 điểm) Cho a, b, c là ba số thực dương thay đổi thỏa mãn:
a + b + c = 3. Hãy tìm giá trị lớn nhất của biểu thức:
F = (a + b)(b + c)(c + a ) - ^ -yfh .

LỜI GIẢI
Câu 1. Hàm số: y = x‘* + —x^.
4 2 _
. Tập xác định; D = R: Hàm số chẵn.
• Sự biến thiên: lim y = - 00.
X->±«
y' = -x^ + 3x = x(3 -x^) = 0<::>x = ±V3 hoặc X = 0.
y' > 0 <=> X = - Vs hoặc 0 < X < -v/s .
Bảng biến thiên: -00 -%/3 0 •J3 + ®
X
y' + 0 - 0 + 0 -
y 9 9
+OỒ ^ 4 -co
^ 4 ^ 0 '
Hàm số đồng biến trên (-oo; -^/3 ), (0;>/3 ) và nghịch biến trên (-V s ; 0),
( yịs ; +Q0). Hàm số đạt CĐ tại (± V3 ; 9/4) và CT tại (0; 0).

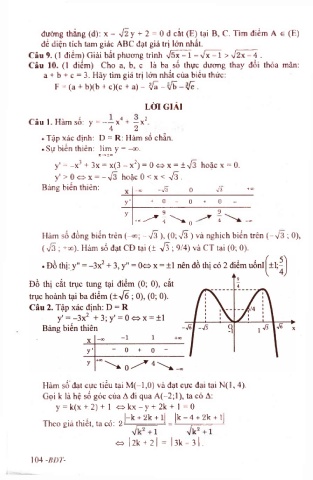
Hàm số đạt cực tiểu tại M(-1,0) và đạt cực đại tại N (l, 4).
Gọi k là hệ số góc của A đi qua A (-2;l), ta có A:
y = k(x + 2 ) + l < = > k x - y + 2 k + l = 0
, | - k + 2 k + l | | k - 4 + 2k + l|
Theo giả thiêt, ta có: 2-— P - I — = - - - - - , - - - - - - — -

« l 2 k + 2 | = | 3 k - 3 l .

\04-BĐT-