Page 359 - Bộ Đề Toán Luyện Thi THPT

LỜI GIẢI
Câu 1.
a) • Tập xác định: D = R.
• Sự biến thiên: lim y = - 00, lim y = +00
X—>-00 X->-K0
Đạo hàm: y' = 3x^ - 3, y' = 0 <=> X = -1 hoặc X = 1.
y' > 0 <=> X e (-oo; -1) u (1; +oo); y' < 0 <=> X e (-1; 1).
Bảng biến thiên: —00 -1 1
X +CC
y' + 0 - 0
y 4 ' '^+00
—00 0

Hàm số đồng biến trên mỗi khoảng (-ũo; -1) và (1; +oo), nghịch biến trên
khoảng (-1; 1).
Hàm số đạt cực đại tại X = -1, ycD = 4 và đạt
cực tiểu tại X = 1, ycT = 0.
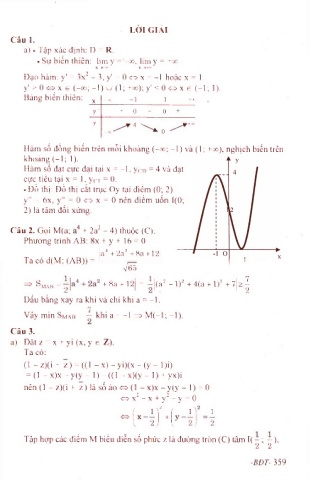
. Đồ thị; Đồ thị cắt trục Oy tại điểm (0; 2).
y" = 6x, y" = 0 <» X = 0 nên điểm uốn 1(0;
2) là tâm đối xứng.

Câu 2, Gọi M(a; + 2a^ - 4) thuộc (C).
Phương trình AB; 8x + y + 16 = 0
_ _ la'*+ 2a'^ + 8a + 12|
Ta có d(M; (AB)) = J ^ I
V 6 5

^ S m a b "" 2 + 8 a + 12| = ỉ|(a ^ - 1)‘^ + 4 (a + 1)'^ + ^1 > -^
Dấu bằng xảy ra khi và chỉ khi a = -1.
7
Vậy min Smab = — khi a = -1 => M (-l; -1).

Câu 3.
a) Đặt z = X + yi (x, y e Z).
Ta có:
(1 -z )(i+ z) = ((l - x ) - y i ) ( x - ( y - l)i)
= (1 - x ) x - y ( y - 1 )-((1 - x ) ( y - l) + yx)i
nên (1 - z)(i + z) là sô ảo o (1 - x)x -y (y - 1) = 0
« x ^ - x + y ^ -y = 0
2
Ci> ( 0 + í l ì 1
l 2j l 2 j 2

Tập họp các điểm M biểu diễn số phức z là đường tròn (C) tâm I( —; —),
2 2

-BĐT- 359